特にこれといった趣味はない私ですが、科学・生物学・数学の雑学が好きです。
（妻には変わってるねと言われました。笑)

特に掘り下げて何かを調べるとか、その分野で何か仕事に繋げようとかは全くないです。
あくまでも知ってるだけでどこにも披露することのない情報だったのですが
最近は仕事以外の時間は結婚式の準備以外は特に何もやっていないので、特にブログに書く内容がないことから雑学について書こうと思います🐈‍⬛

フェルマーの最終定理の歴史と解法

高校数学で一度は聞いたことがあるであろう「フェルマーの最終定理」ですが
最初からそこに定理として存在はしていたけども、そこに至るまでの解法・歴史は知らなかったのでぽちぽちとwikipediaやYoutubeを使って調べてみました。

フェルマーの最終定理の歴史

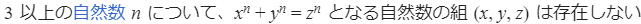
フランスの裁判官のピエール・ド・フェルマーが17世紀に残した命題のことです。
歴史的な命題を残したフェルマーは「数学者」ではなく「裁判官」が本業で、あくまでも数学は趣味の一環だったとされています。
フェルマーは、この定理について本の余白に「私はこれを証明する素晴らしい方法を見つけたが、ここに書くには余白が狭すぎる」とだけ書き残して誰にも解放を伝えることなく亡くなってしまいました。

この謎は、数学者たちを350年以上も悩ませました。フェルマーの時代から、多くの人々がこの定理を証明しようと挑戦しましたが、なかなか成功しませんでした。数式自体はが単純でありながら、証明が困難を極めたことから、数えきれないほどの数学者が頭をひねり、人生を掛けて証明に取り組む数学者が何人も解法にたどり着くことがなかったことから「悪魔の証明」と呼ばれていたとのことです。笑

フェルマーの最終定理の証明

しかし1994年、ついにイギリスの数学者アンドリュー・ワイルズがこの定理を証明しました。
ワイルズは子供の頃からフェルマーの最終定理に魅了され、なんと7年間もひたすら研究室にこもってこの証明に挑んでいました。彼の証明は、現代数学の様々な理論を駆使した非常に複雑なものでしたが、これでようやくフェルマーの最終定理は証明されたのです。

では、ワイルズがどのようにしてこの定理を証明したのか、その方法についても少し触れてみましょう。
ワイルズの証明は、数論と幾何の複雑な理論を組み合わせたものでした。特に重要だったのは、谷山-志村予想という数学の一つの大きな理論です。この予想は、楕円曲線とモジュラー形式という二つの異なる数学的対象が本質的に同じものであるというものです。

谷山-志村予想の内容

谷山-志村予想は具体的にはこうです。
楕円曲線とは、次のような形の方程式で表される曲線のことです

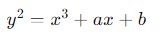
ここで a と b は定数です。楕円曲線は数論や代数幾何学において非常に重要な役割を果たしています。

一方、モジュラー形式とは、特定の変換に対して不変な複素解析関数のことです。
例えば、モジュラー形式 f(z) は、次の条件を満たします

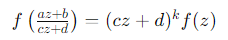
ここで a,b,c,dは整数で、ad−bc=1を満たし、kは整数です。

谷山-志村予想は、任意の楕円曲線が必ずモジュラー形式に対応するというものでした。これは非常に強力な予想であり、数論の深い部分を結びつけるものです。

ワイルズの証明のアプローチ

ワイルズは、この谷山-志村予想がフェルマーの最終定理と密接に関連していることを示しました。
具体的には、フェルマーの最終定理が成り立たないとすると、谷山-志村予想も成り立たないということを証明しました。つまり、もしフェルマーの最終定理が偽であるなら、谷山-志村予想も偽であるということです。

ワイルズはこの関係を利用して、まず谷山-志村予想が成り立つことを証明しました。これにより、フェルマーの最終定理も自動的に成り立つことが示されました。

ワイルズの証明は、以下のような数式を含む複雑な手順を経て行われました

1.リブニッツの条件: 楕円曲線

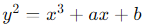
がモジュラー形式に対応するための条件を証明。
2.ヘッケ作用素: 楕円曲線とモジュラー形式の関係を示すために使用される作用素。
3.楕円曲線のフレイ曲線への変換: 特定の楕円曲線がフレイ曲線に変換できることを示す。
4.ガロア表現の理論: 楕円曲線のガロア表現がモジュラー形式に対応することを示す。

（これらについて私はほとんど理解できませんが、これで証明ができるそうです。笑)

証明が発表されたときは、数学界にとってまさに歴史的な瞬間でした。350年以上も未解決だった問題がついに解決されたのですから、これはもう大ニュースです。ワイルズさんの業績は広く称賛され、多くの賞を受賞しました。

フェルマーの最終定理が証明されたことで、数学の世界に新たな扉が開かれたとも言われています。
この証明を通じて、新しい数学的な理論が開発され、それが他の分野にも応用されることとなりました。

フェルマーの最終定理は、単なる数学の問題を超えて、挑戦と情熱の象徴となっています。
数学の世界はもちろんのこと日常生活においても「挑戦すること」の大切さを教えてくれます。

挑戦

出展：いろいろなところ（論文ではないので甘くみてください)
もう少し短くて読みやすい記事はこちら（建築中のおうち一覧)
これを機にもっと詳しくフェルマーの最終定理を知りたい方はこちら

星哉